Hash λ Bye

https://utky.github.io/ に移行したので今後こちらに記事は追加されません

Haskellで再帰的な構文木にFix(不動点)を導入してみる

Haskell GHC compiler

まえおき

例によって僕の記事など読まなくても下記のリンクで解説されているので、 Haskell楽しいなと思う人はこちらをどうぞ。

An Introduction to Recursion Schemes

生きるのに疲れた人は半分白目のゆるい気持ちで以降を読んでね。

Haskellで抽象構文木 (AST) にメタデータを付与する

以前この記事でASTへのメタデータの埋め込み方について少し整理して、 下記のようなアプローチがあることを明らかにした。

  1. メタデータを保存するための値コンストラクタをASTのブランチとして定義する
  2. メタデータを保存するラッパーを定義する

加えて

Fixを使ってなんかファンシーにする

というアプローチについて最後に少し言及した。 これについては当時の僕の頭では理解が追いつかなかったが、 いま少しだけ近づけてきた気がするのでまたしても整理してみる。

導入

僕達は日常的に再帰的な構文に出くわしている。

ラムダ項の定義とかもうまさしくそれ。

t ::=
    x
    λx. t
    t t

型システム入門のP.40から拝借

Haskellで書くと、例えばこうなる。

type Id = String

data Term
  = Var Id
  | Abs Id Term
  | App Term Term
  deriving (Eq, Show)

問題

素朴に記述したこのAST。 使っているうちに構文木そのもののデータだけでなく、メタデータを保存していきたくなる。

メタデータの例

  • ソースファイル名
  • ファイル内の位置情報

普通にアプローチするとこのASTの定義を改造してメタデータを埋め込める場所を用意する。

例えばトークンの開始位置と終了位置を含むデータ Region を埋め込む例の場合。

data Term
  = Var Region Id
  | Abs Region Id Term
  | App Region Term Term
  deriving (Eq, Show)

しかし、これだとASTのデータ型は純粋な構文 以外 のデータも持つことになってしまう。 できればメタデータをASTをに混ぜるのではなく、分離した上で自然に組み合わせたい。

ということでその立役者となる Cofree を目指すことになる。

しかし、そもそも Cofree の下地となっている Fix という構造がよく解らなかったので、この記事ではまず下記のポイントを確認していこうと思う。

  1. Fix とはなにものなのか
  2. Fix を導入するとなにが起こるのか

再帰的な構文の抽象化

data Term
  = Var Id
  | Abs Id Term   -- 再帰あり
  | App Term Term -- 再帰あり
  deriving (Eq, Show)

もう一度構文定義を再掲。 3つ中2つのコンストラクタは再帰的に Term を受け取るようになっている。

たとえば Abs は具体的なデータとして Term を再帰的に内包できる。

この再帰構造はもう一段抽象化できる。 型変数を導入することで下記のようになる。

data TermF a
  = VarF Id
  | AbsF Id a
  | AppF a a
  deriving (Eq, Show)

コンストラクタの中で Term を持っていたところを型変数 a に括りだした形になる。 型をみると解るように、carrier typeを持つこのデータ型は Functor になることができる。 言語拡張の DeriveFunctor , DeriveTraversable , DeriveFoldable を使うことで、 このデータ型はとても多くの性質を獲得できるようになる。

これで具体的な項を作ってみる。

> let absx = AbsF "x" $ VarF "x"
> :t absx
absx :: TermF (TermF a)
> let absxy = AbsF "x" $ AbsF "y" $ VarF "y"
> :t absxy
absxy :: TermF (TermF (TermF a))

こんな感じ。

項がネストする深さに応じて型もネストしている のが解る。 10の深さの項を作ると、

TermF (TermF (TermF (TermF ...)))

とTermFが10個続いていくことになる。 でもこれは扱いにくい。 構成するデータに応じて型が変わり過ぎる。

古いバージョンの定義を使って項を構成して見比べてみよう。

> let absx = Abs "x" $ Var "x"
> :t absx
absx :: Term
> let absxy = Abs "x" $ Abs "y" $ Var "y"
> :t absxy
absxy :: Term

型が単純。

型変数を導入する前はどんな構成方法でも項の型は Term だった。 しかし型変数を導入したら、構成方法によって型が変わってしまった。

実はこれでは充分ではない。 ネストする、つまり再帰する型を一つの型に収束させる必要がある。

イメージ的には、

TermF (TermF a) -> TermF
TermF (TermF (TermF a)) -> TermF

のようにネストした型を TermF みたいな何か単純な表現に収束してくれるものを求めている。

Fix

ここで奇妙なデータ型を導入する。

newtype Fix f = In (f (Fix f))

定義方法はこちらに従った: Understanding F-Algebras

複雑な型を内部にもっており、僕も最初に見た時は面食らった。

この Fix を使うと先ほどの再帰的にネストしていく型を収束できる。 ただしデータの構成時にちょっとおまけが必要。

> let absxfix = In $ AbsF "x" $ In $ VarF "x"
> :t absxfix
absxfix :: Fix TermF

お、型のネストが消えた。 読みやすさのために括弧を使ってみる。

> let absxfix = In ( AbsF "x" ( In ( VarF "x" ) ) )
> :t absxfix
absxfix :: Fix TermF

TermF を構成したら必ず In でラップしてやるのがミソ。
すると Fix TermF という型が表れて再帰を隠してくれる。 もう少し深い項を構成してみよう。

> let absxyfix = In $ AbsF "x" $ In $ AbsF "y" $ In $ VarF "y"
> :t absxyfix
absxyfix :: Fix TermF

やっぱり Fix TermF に収束した。

収束の過程・仕組み

単純に型合わせの過程を観察して、確かに Fix TermF になることを見てみよう。

と言いつつ気力が湧いてきたら書く (ごめんなさい)

Fixは型レベルのfixだった

Fix はデータ型だけどこれと同じような定義を持つ関数がある。

Control.Monad.Fix.fix

型はこんな感じ。

> :t fix
fix :: (a -> a) -> a

関数を渡すと値が出てくる変なヤツ。

一方でFixの種 (kind) はどうだろうか？

> :k Fix
Fix :: (* -> *) -> *

似すぎ。

もしやと思ってそれぞれの定義を見比べる。

まずfixの定義。 ( こちらを参照 )

fix :: (a -> a) -> a
fix f = f (fix f)

再帰的に呼び出す fix f の結果に f を適用している。

newtype Fix f = In (f (Fix f))

再帰的に呼び出す Fix f の結果に f を適用している。

一緒じゃん。

形が似ていることは解った。 fix を既に知っている人にとっては Fix の振る舞いはもはや疑問の余地がないものだろう。

ただ僕はよく解らないのでちゃんと考える必要がある。

Fixは何なのか

下記のリンクを読めば解る人には解るかもしれない。

HaskellWiki - 不動点と再帰

僕は解らない。

試してみた僕の理解だと Fix f とは

fを再帰的に適用して収束するとこを見つける関数のようなもの

という認識。

Fix f とするとき、 Fix の定義により

Fix f = f(f(f(f(...))))

となる。 再帰的に型コンストラクタ f を適用していくことを表現している。

この Fix というデータ型と似た関数版もやはり再帰に関わる。

Control.Monad.Fix.fix

fix f = f(f(f(f(f(...)))))

こうなる。 こちらも同様に関数 f を再帰的に適用していくことを表現している。

データ型版も関数版も再帰的に f を再帰的に適用することを表現しているのがポイント。

Fixで得たもの・失ったもの

Fix を使うことで任意の深さで再帰する型 (例えば TermF ) を同一の型で表現することができるようになった。 この統一的な表現方式により、冒頭のリンクで言及されているような

  • 再帰的なデータの走査
  • データ構造の再帰と作用の分離

などを手にすることができる。

この Fix によってもたらされた恩恵の向こうに Cofree が待っているようだ。

得たもの

Cofreeという抽象構造へのステップ。 あと少しっぽい。

うまくいけばASTにメタデータを きれいに 載せられるかもしれない！

失ったもの

単純に項を構成する方法。 Fix導入前は項を構成して比較することも容易だった。

> ( Abs "x" ( Var "x" ) ) == ( Abs "x" ( Var "x" ) )
True

なのでテストを書くのが楽だった。

ところが今回は Fix で構文データをラップする必要が出てくる。

しかしFixという構造自体はEqのインスタンスにできなさそう。同値という性質を定義できない。 なのでFixを使って作られた項は単純な比較ができなくなる。

2019-03-03

コメントにて Fix の同値性は定義できる旨をアドバイス頂いたので検証。 ご指摘の通り Fix の導入にあたり前述のようなデメリットは無いと分った。

import Data.Functor.Classes (Eq1, eq1)

instance Eq1 TermF where
  liftEq _ (VarF i) (VarF j) = i == j
  liftEq f (AbsF i x) (AbsF j y) = i == j && f x y
  liftEq f (AppF a b) (AppF c d) = f a c && f b d
  liftEq _ _ _ = False

instance (Eq1 f) => Eq (Fix f) where
  (In x) == (In y) = eq1 x y

上記のように2つの定義、すなわち 1. TermF に Eq1 2. Fix f に Eq を与えることで同値性のテストもできるようになる。

*Main Lib Data.Functor.Classes> lhs = In $ AbsF "x" $ In $ AbsF "y" $ In $ VarF "y"
*Main Lib Data.Functor.Classes> rhs = In $ AbsF "x" $ In $ AbsF "y" $ In $ VarF "y"
*Main Lib Data.Functor.Classes> lhs == rhs
True

こんな風に Fix で包んだ項も比較できる。

GHC 8.6系から使える QuantifiedConstraints を使ってさらに無駄なく定義できるかは確認中。

  • Eq (Fix f) を定義するためには Eq f を仮定したい
  • Eq fを仮定したいところだが f はカインドが * -> * なので Eq (f a) を仮定しようとする (ここが自信ない)
  • Eq (f a) を仮定することで導入される型変数 a が、定義　Eq (Fix f) に現れないためにエラーとなる
    * Variable `a' occurs more often
        in the constraint `Eq (f a)' than in the instance head `Eq (Fix f)'
      (Use UndecidableInstances to permit this)
    * In the instance declaration for `Eq (Fix f)'
   |
31 | instance Eq (f a) => Eq (Fix f) where
   |          ^^^^^^^^^^^^^^^^^^^^^^
   |

Free f a みたいなデータ型に Eq のインスタンス定義を与えるならいけそう。

FixやCofreeは本当に必要か？

エレガントに見えるけど率直さを失った。 本当に必要な抽象か？

比較してみる

1. メタデータを保存するための値コンストラクタをASTのブランチとして定義する

ASTに位置情報という付加情報のためのブランチを作る。 簡単、率直だが美しくはない。

ASTの規模が小さいならブランチを作るコスト、それらを分解するコストは大したことないのでこれでいい。 というかSML/NJがこれを導入している実績あるので、 同程度の規模ならなんとかなると思っていいんじゃないかな。

人生はエレガンス、がスローガンの人だけ次を読むべき。

2. メタデータを保存するラッパーを定義する

位置情報を保存するラッパーを作る。 ASTそれ自体の定義はピュアに保てる。

今回の Fix も所詮ラッパーなので導入コストについていえば、実は2と変わらなかったりする。 その上で構文が Functor や Traversable Foldable を備えるなら 応用力では今回の Fix アプローチが勝る。

と、言えなくもない。

ただし、僕はこの Fix ベースの構文定義を使っている実用的なプログラミング言語をまだ目撃していない。 事例が無いので何か本質的な瑕疵でもあるのでは、と恐怖している。

誰か Fix 使った構文定義しているプログラミング言語実装の例を知っていたら教えてほしい。

うそ。教えてなくてもいい。 僕が Fix の餌食になるので。

まあ、せっかく学んだのでこのアプローチを簡単に捨てるのはまだ少し惜しい気もしている。 ということで、もう少し調査を続行。

次の話題

どうもこの手法、 Recursion Scheme と呼ばれるアプローチらしい。

An Introduction to Recursion Schemes

ということで冒頭のリンクにたどり着いたのだった。

この記事の基礎になっている論文が下記。

Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire

木構造の簡約・走査に関連する発想の一つみたいだ。 読みたい。読もう。

直近の懸念は、この Fix を導入したとして、 派手に壊れたテストをどうやって直して行くか、だ。

その問題に対して何かヒントがあるか拾っていきたい。

最近

ずっとvtuberの動画観てる。

  • ときのそら
  • ぜったい天使くるみちゃん (もう活動一時停止してる)

歌う人好きっぽい。

(技術の話をして)

Haskellで抽象構文木 (AST) にメタデータを付与する

Haskell GHC compiler Elm SML StandardML parsec

2018-01-04 追記: ここで全部語り尽くされている気がしたので、Labelling AST Nodes with locations なにもこんなブログ読むことはないのかもしれない。

megaparsecを使って構文解析器を書いている。

構文解析やっているとASTにソースファイルの位置情報とかをメタデータとして乗せたくなるが、 どんな感じで実装するのか調べた。

僕自身はどのアプローチをとるのか決まっていない。

問題

やりたいこと

megaparsec, parsecなどのコンビネータライブラリはジェネレータ系のalex + happyと比べると幾分まともなエラーメッセージを吐くようになっている。(alex + happyがえげつないほどterseなだけ)

しかし、構文解析が終わった後のα変換によるshadowingの回避や型推論のフェーズでコンパイラがエラーを見つけた場合に、 そのトークンの位置が保存されていないと、エラーメッセージとして不親切に思う。

なので、ASTに位置 SourcePos のようなものを乗せたい。

解きたいこと

しかし、単純に既存のデータ構造に埋め込むと、値コンストラクタのArityが変わったり、コンストラクタのパターンが増えたりしてせっかく書いたhspecのテストも盛大に直さなければならない。

それは嫌だ。

僕がやりたいのは 「ASTにメタデータとして位置情報を乗せたい」 のであって 「ASTの意味を変えたい」 訳では断じて無い。 僕がやりたいことを簡潔にデータ型として表現したい。

おい、Haskellお前ならできるはずだろ！？

夢を見させてくれよ！

お前そういうの得意だろ！？

アプローチ

少し既存の構文解析器を調べた。

下記の調査をまとめると。

  1. メタデータを保存するための値コンストラクタをASTのブランチとして定義する
  2. メタデータを保存するラッパーを定義する

の2種類のアプローチを観測した。

1. ASTにブランチを追加するパターン

下記の2言語で発見。

dhall-haskell

Note というコンストラクタをメインのASTにブランチとして定義して、 s にメタ情報を格納しているらしい。

    -- | > Note s x                                 ~  e
    | Note s (Expr s a)

s が位置情報を含んでいる模様。

ASTがプログラミング言語の構文を定義するのだとすると、 こういったメタ情報がコンストラクタに表れるのはやはりノイズでしかないので できれば排除したいなーという思い。

SML/NJ

fixitem というデータ型を定義している

type 'a fixitem = {item: 'a, fixity: symbol option, region: region}

この region というのが場所を保存している。

でそれをASTのコンストラクタに埋め込んでいる。

  | FlatAppExp of exp fixitem list (* expressions before fixity parsing *)

あるいは位置保存用のコンストラクタを各サブツリーのデータ型に定義している。

  | MarkExp of exp * region   (* mark an expression *) |

この MarkXXX とつくコンストラクタは全て位置情報を確保しておくためだけにある、 メタな何かだ。

式やパターンなどのASTごとにこういった MarkXXX というコンストラクタを定義している。

これはdhallと同じアプローチのようだ。

2. ASTにラッパーをかぶせるパターン

下記の2言語で発見。

ghc

概ね知りたいことがWikiに書いてあった。

The HsSyn types

ghcマジ天使。

  • SrcLoc というのが位置情報を持っている。
  • SrcSpan というのが位置から位置までのブロックを表している
  • Located e で e の実際のブロックを保存する
-- | We attach SrcSpans to lots of things, so let's have a datatype for it.
data GenLocated l e = L l e
  deriving (…)

type Located e = GenLocated SrcSpan e

ghcではなんらかのASTを構築したら、これを Located で包むことによって、 位置情報を付加している。

この場合、ASTそれ自体 (この場合HsSyn) の定義は変わらないので 関心事は上手く分離されているといえる。

elm-compiler

ghcと同様の方式を選んでいるように見える。

これは式のASTの例だが、

-- EXPRESSIONS


type Expr def =
    A.Located (Expr' def)


data Expr' def
    = Literal Literal.Literal
    ...

Expr' が実際のAST。( def はbinderっぽいので気にしなくてよし)

それに Located というデータをかぶせている。

これは何かというと、

-- ANNOTATION


type Located a =
    Annotated R.Region a

Located はペイロードとして a この場合は Expr' とともに、 Region を持つようになっている。

data Region =
  Region
    { start :: !Position
    , end :: !Position
    }
    deriving (Eq, Show)

Region がまさしく位置情報。

ghcと同じアプローチを感じる。

(発展的話題) なんか色々言ってる人がおる

おもむろに怪しい道具 Fix を持ち出す海外勢の様子。

How to work with AST with Cofree annotation?

Adding source positions to AST nodes for free

何やってるのかわからない。

どいつもこいつも Fix 大好きだなおい。 本気で言っているのか。

それは本当にお前たちの問題領域を簡潔に保っているのか。

という疑念が晴れない。 というか、ここにわざわざFreeモナドを導入する必要はあるのか。 ぶっちゃけ使いたいだけじゃないのか。

ダークパワーを使いたくない僕としてはまだこのアプローチにだいぶ抵抗感がある。

どうするどうする

どうしよう。

ASTそのものは定義を変えずにいけるghc方式をとるかもしれない。

だいぶ素人なので詳しい人いたらアドバイスください。。。

まとめ

ASTに位置情報を付与したい場合は

  1. メタデータを保存するための値コンストラクタをASTのブランチとして定義する
  2. メタデータを保存するラッパーを定義する

という方法があるらしい。

(その他、識別子から位置情報を引くハッシュテーブルを作るみたいなのもあった気がする)

プログラミングClojureにおける「データ」とは何か

Clojure programming

プログラミングClojureは僕が読んだ二冊目のClojureの本で、 Clojureがどんな機能を備えているのか、どんなパラダイムなのかを 教えてくれるとても良い本。

読み終わった今でも時々、「あそこどう書いてたっけな」と気になってはすぐに読み返してしまう。

しかしながら、何度読んでも"具体的なオブジェクト"と"データ"という記述の違いが解らなかった。 その後、ひとりで悩んだり、人に相談してようやく理解できた。

この記事ではその理解をなんとか噛み砕いて説明しようと思う。

「データ」

どんなワークフローでプログラムを組んでいくのがよいか

プログラミングClojureではそれについて説明している箇所がある。 誰もが気になるところだ。文法や言語の機能が解ったところで、「実際どうやるの？」が解らなければ勇気をもって実装に踏み出せないものだ。

例えばこんな文章で説明されている。

Clojureでの設計の肝は、いつでもどこでも具体的なオブジェクトで溢れさせるのではなく、データそのものについて考えることだ。

引用元: 10.1 Clojurebreaker ゲームのスコアの計算 p.222

これが解らなかった

「データそのもの」とはなんだろうか。 具体的なオブジェクトとの違いは何だ？

さらにClojureプログラミングの原則として下記のようなことが書いてある。

・領域特有の具体物を持ち込まない（データはデータとして扱う）。

引用元: 10.1 Clojurebreaker ゲームのスコアの計算 p.224

これも解らなかった

「データはデータ」？ データは具体物ではないのか？ では何なんだ？

何が難しいのか

  • 具体的なオブジェクト/具体物
  • データ

この違いが解っていないから混乱する。もう一度文章をよく睨んでみよう。

Clojureでの設計の肝は、いつでもどこでも具体的なオブジェクトで溢れさせるのではなく、データそのものについて考えることだ。

データそのものについて考える。 それは具体的な何かの概念について考えることになるだろう。

そう思った。というか、そう連想した。

なので

データそのものについて考える＝具体的なオブジェクトを設計する

ではないの？

・領域特有の具体物を持ち込まない（データはデータとして扱う）。

領域特有の具体物を持ち込まないプログラミング、というのが想像できなかった。

データが具体的でないのなら、いったいどんな形をしているのか、まったく解らない。 データは「扱われる」のだから何らかの意味で具体的になっているはずだろう。

教えてもらった

ずっと考えていても解決する兆しが無いので、直接訳者の方に質問してみた。

解ったこと

頂いた回答をもとにまとめると。。。。

具体物

{ :name "津島善子" :blood-type O :birth-day [Jul 13] }

データ

{ :name "津島善子" :blood-type O :birth-day [Jul 13] }

!?!?!?

同じっ！？

記法は同じ！！

しかし意味が異なる！！

どちらも同じMapだが、

  • 具体物としてそれを捉えた場合: それは津島善子という人の情報を表す
  • データとしてそれを捉えた場合: それはkey-value pairsを表す

「どう捉えるか」という解釈が問題。

それは確かに人を表す情報かもしれないけど、 それはいったん忘れて Map (key-value pairs) という データ として関数を適用しよう。

再咀嚼

Clojureでの設計の肝は、いつでもどこでも具体的なオブジェクトで溢れさせるのではなく、データそのものについて考えることだ。

・領域特有の具体物を持ち込まない（データはデータとして扱う）。

これらは何を言っているか。

対象の具体的な意味は忘れて、Map, Seq, Vectorとしてデータを変換するようなAPIを設計しよう、ということだ。 そして幸いにも clojure.core にそういった関数が膨大にある。 それを使えばいいじゃないか。

そう、それが再利用性ということ。

必要であれば自分で少し拡張しないといけないかもしれない。

具体的なオブジェクト

たとえばこれは明らかに具体物だ。

(defrecord AqoursMember [name blood-type birth-day])

だって AqoursMember と書いてある。 それが見たまんま ラブライブ サンシャイン に出てくるスクールアイドルを示す何かであることは疑いようもない。

データ

一方でそれは

IPersistentMap

だ。

それは key と value の対が収まった不変データそのもの。 歌ったり汗をかいたりはしない。

ただ assoc や map や reduce に渡せるインタフェースを満たすデータ構造だと考えることができる。

意味を忘れるとはつまり、それが僕達の仕事の中でどんな意味を持つかではなく、Clojureのプリミティブとして何であるかだけを考える、ということ。

データが何を意味するかは気にする必要ない。一般化して考えよう。

それがClojureにおけるボトムアッププログラミングのスタイルである、ということらしい。

現実的な問題に立ち向かう

そうは言っても僕達は具体物・具象から離れてはアプリケーションを作れない。 アプリケーションが特定の問題解くものである以上、絶対に避けられない。

そこで、Clojureのプログラミングではデータという抽象を扱うたくさんのAPIの 上に あるいは その外側 に領域特有(Domain Specific)のプログラムを構築する。

僕個人としてはこの考え方は結構衝撃的だった。

ドメインがいる場所

DDDを少しかじってみるとHexagonal Architectureというものに出くわす。

僕はアプリケーションの俯瞰図をそのイメージで考えることが多い。

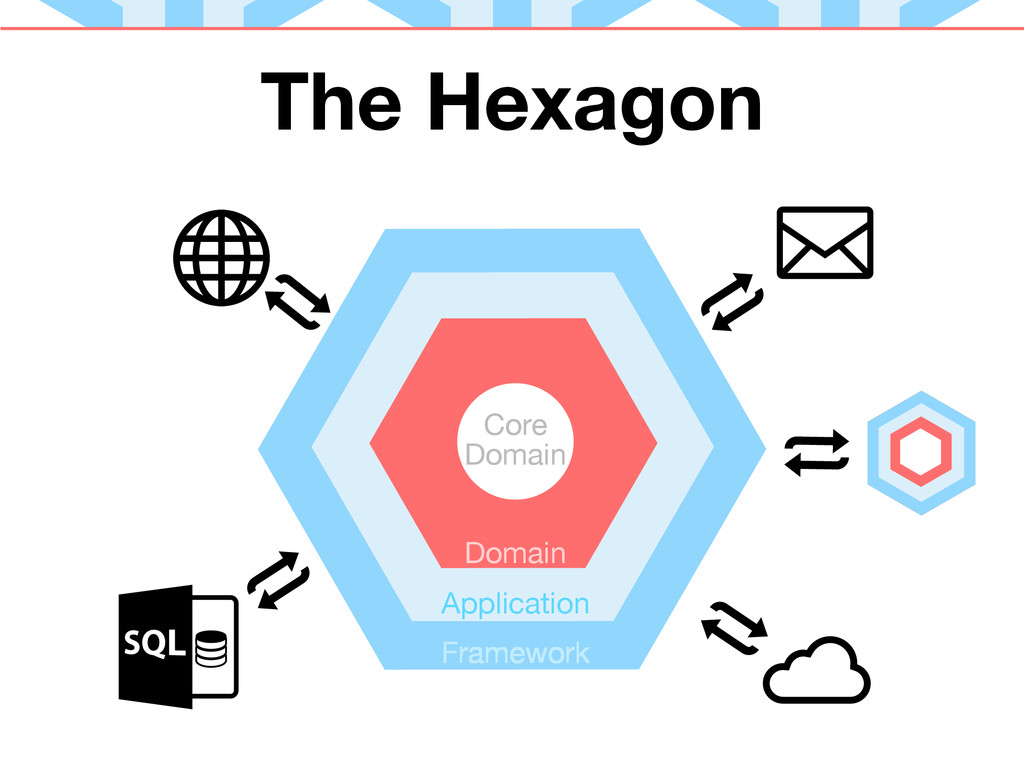
Hexagonal Architecture

この図だと、ドメインつまり具体的なオブジェクトの集まりはアプリケーションの中核にいる。

でもClojureのワークフローに従うとこの中と外が 逆転 する。

f:id:ilyaletre:20180101120422j:plain

ドメイン固有のオブジェクトは外側になる。

代わりに中核に居座るのは抽象データを操作する関数だけになる。

ボトムアップでコアを作っていく

ボトムアッププログラミングと口にする時、それはこの抽象データ用の中核を作っていくことに他ならない。 定義する関数が Person だとか AqoursMember だとか、そういうことは一切気にしないでプログラミングする。

勿論REPLでテストデータを渡すために仮のレコードを定義して使うことはあるかもしれないが、 呼び出される関数はそれらをただの Map として認識して操作する。

この一般化された関数を"ボトム"として、その上に少しずつ具体的な"トップ"を作っていく。

あるいは

この一般化された関数を"内側"として、その"外側"に少しずつ具体的なオブジェクトを作っていく。

まとめ

プログラミングClojureにおける"具体"と"データ"の違いを見てきた。

  • 具体/具象: ドメイン固有オブジェクトとしてそれを捉えた時の呼び方
  • データ/抽象: ドメインをいったん忘れてただのClojureのデータ構造としてそれを捉えた時の呼び方

ボトムアッププログラミングとは、

  • データを操作する関数を最初に作り、
  • そこから具体的な意味を扱う関数をその上に作る

ようなワークフローである。

ということが解った。

謝辞

訳者の川合史朗さんの適切なアドバイスを受けてなんとかこの理解を得ることができました。 ありがとうございました。

ところで

原著の第三版 が出ている。

transducerとspecについての内容が追加されているらしく、もう原著で買うか、という気分になっている。

Left Recursionの悪夢再び

Haskell

はじめに

Happyで生成したパーサのコンパイル遅すぎてもう限界だったのでparser combinatorに戻ってきた。

そしてまた現れたのだ、やつが。。。。

問題

やろうとしてることは以前と変わらない。

SML Definitionを読んで型の注釈を表す式 ty を解析しようとしているが、 左無限再帰が起きてしまって解析が終了しないというもの。

ty ::= tyvar            (1) type variable such as 'a
       { tyrow i }      (2) record type
       tyseq longtycon  (3) type constructor with type arguments
       ty -> ty         (4) function type

tyseq ::= ty                  (5) singleton
                              (6) empty
          (ty1, ty2, ... tyn) (7) list of type

ここの (3) を解析する時にで遭遇するのがLeft Recursion(左再帰)問題。

ty という構文を解析する際に、(3)の type constructor のサブツリーを作ろうとする場合を考える。

この時、まずは tyseq を解析するステップに入る。 tyseq のEBNFを見ると明らかなようにこれは問題がある。

  • (5) の場合は更に ty に解析を開始するため左再帰が無限に下降する。
  • (6) はmegaparsecの option を使えば表現できると思われる。
  • (7) カンマ区切りの型のリストだが結局これも ty の解析に入るので無限再帰する。

となるため確実に無限再帰に陥る。

よくブログ記事見かけるアドバイス

Text.Megaparsec.Exprを使えと言われる。

このモジュールは二項演算子や単項演算子で左再帰が発生する場合でも上手く取り扱ってくれる。

これを活用できないかと考えた。

--      ↓引数となる式
        tyseq longtycon
--            ↑後置単項演算子

こんな感じで捉える。

と思ったがこれを率直に実装するのは難しいと解った。 なぜなら型が合わないから。

このtype constructorの構文をADTのコンストラクタで表現するならこうなる。

TTyCon [Ty] TyCon

TyCon が後置演算子そのものを格納し、 [Ty] が先行する tyseq を格納する。

このコンストラクタの型は [Ty] -> TyCon -> Ty となる。

が前述のモジュールでは後置演算子になれるコンストラクタは Ty -> Ty である必要がある。

少なくとも手持ちのコンストラクタは [Ty] だがライブラリが期待するのは Ty なのでどうも合わない。

というところで今日は終了。

これから

いやー厳しい戦いだ。

あんまり基礎的なところが解っていないっぽいので異様に解決まで時間くうことが容易に想像できる。

GHCの中間言語Coreへの脱糖を覗き見る

Haskell GHC programming compiler

Haskell (その3) Advent Calendar 2017 11日目の記事。(予約投稿知らなかったのでフライングになった)

GHCがコンパイルの途中で中間表現として用いるCoreの生成っぷりを観察する。

観察して、あーはいはいなるほどね(わかってない)、と言うだけになりそう。

はじめに

GHCはHaskellのソースコードを低レベルなコードへとコンパイルする過程で様々なpass(コンパイルのステージ)を通じてプログラムデータを変換する。 俯瞰図は下記のリンクに詳しい。

Compiling one module: HscMain

僕がGHCの話をどこかで聞きかじってかっこいいな、と思ったのは、 GHCがコンパイラの中間言語として定義しているCoreを知った時。

このCoreと名付けられた中間言語はDesugar passにて生成され、下記のような性質を持っている。

  • 小さな構文
    • 3つのデータ型と15の値コンストラクタ
  • 束縛変数には全て型がついている
    • 前段で推論されている
  • 全て型がついているため高速に型検査ができる
    • もう推論は終わっているので検査が高速
  • 単純だが大きな表現力を持つ

GHCはリリースのたびに様々な言語拡張が増えていて、 表面上の構文は多様になってきている。 それにも関わらずこのCoreという中間言語は下記のような小ささを保っている。

  • 3つのデータ型
  • 15の値コンストラクタ

ghc-8.2.2 CoreSyn

data Expr b
  = Var   Id
  | Lit   Literal
  | App   (Expr b) (Arg b)
  | Lam   b (Expr b)
  | Let   (Bind b) (Expr b)
  | Case  (Expr b) b Type [Alt b]
  | Cast  (Expr b) Coercion
  | Tick  (Tickish Id) (Expr b)
  | Type  Type
  | Coercion Coercion
  deriving Data

data AltCon
  = DataAlt DataCon 
  | LitAlt  Literal
  | DEFAULT
   deriving (Eq, Data)

data Bind b = NonRec b (Expr b)
            | Rec [(b, (Expr b))]
  deriving Data

type Arg b = Expr b
type Alt b = (AltCon, [b], Expr b)

各値コンストラクタが依存している更に細かいデータ型はあるにせよ、 Haskellのソースコードは上記のデータ型にdesugar(脱糖)されて単純化される。

正直、僕もすべてのコンストラクタの意味が解っているわけではない。 しかしあの多彩な表現力を持ったHaskellの構文が この小さなCoreに変換可能である ことに大きく驚いた。

ここではこれらのデータ型の詳細には立ち入らず、 実際にHaskellのプログラム書きながらこのdesugarされたCoreがどう変化しているかを見てみようと思う。

観察してみる

この節ではGHCのデバッグオプションを使って、 parseされたプログラムがDesugar passを経た後の結果を確認してみる。

どんな感じで見えるんだろ。

Setup

stack.yamlにオプションをつけておこう。

ghc-options:
  "*":  -ddump-to-file  -ddump-ds -ddump-simpl -dsuppress-idinfo -dsuppress-coercions -dsuppress-uniques -dsuppress-module-prefixes

長い。長いけれどポイントは -ddump-ds のみ。 -dsuppres 系は冗長な出力を減らすために指定しているだけ。

このオプションをつけておくとstackのビルドの成果物を格納する .stack-work ディレクトリの下にレポートが出力される。

今回 src/Lib.hs に定義を書き下しているため出力結果は

.stack-work/dist/x86_64-linux-nix/Cabal-1.24.2.0/build/src/Lib.dump-ds

というファイルに出力される。

定数

stringConst :: String
stringConst = "Hello"

-- RHS size: {terms: 2, types: 0, coercions: 0}
stringConst :: String
stringConst = unpackCString# "Hello"#

まあ、なんか、うん。そうだよね。

関数適用

falsy :: Bool
falsy = not True

-- RHS size: {terms: 2, types: 0, coercions: 0}
falsy :: Bool
falsy = not True

変化なし。単純過ぎたか。

Infix

two :: Int
two = 1 + 1

-- RHS size: {terms: 6, types: 1, coercions: 0}
two :: Int
two = + $fNumInt (I# 1#) (I# 1#)

なにか起きた。。。

二項演算子も結局は関数なので、 + 1 1 のようなS式っぽい見た目になるのはわかる。

$fNumInt という謎のシンボルが出てきた。

後でも出てくるが型クラス Num の Int インスタンス定義を渡している模様。

関数合成

notNot :: Bool -> Bool
notNot = not . not

-- RHS size: {terms: 3, types: 3, coercions: 0}
notNot :: Bool -> Bool
notNot = . @ Bool @ Bool @ Bool not not

x . y が . x y に変換された。 これもまた二項演算子が2引数の関数に変換されている。

だけではなくて @ Bool なる記号が出てくる。 これは . が持つ多相性に関連する。 次で説明。

多相関数

identity :: a -> a
identity x = x

-- RHS size: {terms: 3, types: 3, coercions: 0}
identity :: forall a. a -> a
identity = \ (@ a) (x :: a) -> x

ちょっと形が変わった。大事なところにきた。

Haskellで匿名関数と作る時は

\ x -> x

とする。

なので

\ (x :: a) -> x

となるなら解る。 「aという型を持つxという値を受けとり、そのxを返す」というような意味で読める。

しかし実際は

\ (@ a) (x :: a) -> x

こう。

(@ a)

匿名関数に引数が増えている。

これは 型変数が関数の仮引数として定義されている ことを表す。

とても不思議。

-- 型    値
\  (@ a) (x :: a) -> x

型と値が同列の引数として扱われていることになる。

Coreでは型の引数と値の引数が同列に扱われて関数に適用される。

なのでこの関数に引数を適用する場合は、

identity Int 1

のようにして型引数が決定され、値引数が決定されているものと思われる。

補足: forall について

identity :: forall a. a -> a

forall が表れるが意味的にはもとの a -> a となんら変わらない。 糖衣構文として forall の省略が許容されていたものが、 脱糖を経て明示化されただけ。

補足: Core上の表現

この関数がCore上でどう表現されているかというと

Lam (TyVar "a") (Lam (Id "x") (Var (Id "x")))

ラムダ計算っぽく書くと

λ a. λ x: a. x

こんな感じ? (解らないけど a にはkindとして * でもつくのかな？)

1つめのラムダ抽象の引数は型で、 2つめのラムダ抽象の引数はa型の値xとなる。

この2つの引数はCore言語内で Var という型を持つ。

Var

型と値が同列で引数になる仕組みは簡単で、 関数の引数に束縛されるデータ型 Var が下記のようになっているから。

data Var
  = TyVar ...   -- 型レベルの変数
  | TcTyVar ... -- 不明 "Used for kind variables during inference" らしい
  | Id ...      -- 値レベルの変数

この関数の引数に与えられるデータが

  • TyVar: 型
  • Id: 値

どちらも受け付けるようになっている。

多相関数の適用 (型変数が決定されるのか？)

本当に型も引数として関数に適用されているのかを観察。 先程の多相関数に引数を適用してみる。

one :: Int
one = identity 1

-- RHS size: {terms: 3, types: 1, coercions: 0}
one :: Int
one = identity @ Int (I# 1#)

予想通り。

@ Int で確かに型を適用している。

高階関数

おなじみの関数合成。

comp :: (b -> c) -> (a -> b) -> a -> c
comp f g x = f (g x)

-- RHS size: {terms: 9, types: 11, coercions: 0}
comp :: forall b c a. (b -> c) -> (a -> b) -> a -> c
comp =
  \ (@ b) (@ c) (@ a) (f :: b -> c) (g :: a -> b) (x :: a) -> f (g x)

引数がお化け。。。。

だけれど、型変数の抽出ルールはやはり明確だ。

型変数は b c a の順で登場する。 それに合わせて forall b c a の順で定義される。

さらに forall に続く型変数はCoreのラムダ抽象で引数になる。

パターンマッチ

hasValue :: Maybe a -> Bool
hasValue (Just _) = True
hasValue Nothing  = False

-- RHS size: {terms: 8, types: 7, coercions: 0}
hasValue :: forall a. Maybe a -> Bool
hasValue =
  \ (@ a) (ds :: Maybe a) ->
    case ds of _ {
      Nothing -> False;
      Just _ -> True
    }

関数定義部におけるパターンパッチはcase of構文に変換されている。

CoreのCaseコンストラクタに変換されているらしい。

Case  (Expr b) b Type [Alt b]

実はこのコンストラクタ b と Type の部分がまだ何者か判明していない。

b が Expr b を束縛しており、 Type が [Alt b] の式の型を注釈している？

型クラス制約

型クラスつきの関数を定義するとどうなるだろうか。

join :: (Monad m) => m (m a) -> m a
join = (>>= id)

-- RHS size: {terms: 8, types: 17, coercions: 0}
join :: forall (m :: * -> *) a. Monad m => m (m a) -> m a
join =
  \ (@ (m :: * -> *)) (@ a) ($dMonad :: Monad m) (ds :: m (m a)) ->
    >>= @ m $dMonad @ (m a) @ a ds (id @ (m a))

斬新な変数が出てきた。 引数部分を分解して一つ一つ読み解こう。

(@ (m :: * -> *))    -- Monadのインスタンスとなるべき型
(@ a)                -- mで修飾された入力値の型の一部
($dMonad :: Monad m) -- 型クラスを満たすインスタンスの定義
(ds :: m (m a))      -- 実際の関数の入力値

join に表れる型変数は m と a 。

なのでその2つは最初に (@ (m :: * -> *)) と @ a として束縛される。 (ds :: m (m a)) は実際の関数の引数なので疑問なし。 問題は ($dMonad :: Monad m) というどこから出てきたのか解らない束縛。

これは型クラスのインスタンスも関数の引数として受け取るための束縛らしい。

ということは、型クラスのインスタンスを渡しているところも見られるかもしれない。。。

型クラスのインスタンス適用

さきほど定義した join を使ってみよう。

maybeOne :: Maybe Int
maybeOne = join (Just (Just 1))

-- RHS size: {terms: 6, types: 5, coercions: 0}
maybeOne :: Maybe Int
maybeOne =
  join
    -- (@ (m :: * -> *))
    @ Maybe
    -- (@ a)
    @ Int
    -- ($dMonad :: Monad m)
    $fMonadMaybe
    -- (ds :: m (m a))
    (Just @ (Maybe Int) (Just @ Int (I# 1#)))

コメントで先程の join の定義と対照してみた。

Monad のインスタンス定義を受け取る部分には

$fMonadMaybe

が。

名前から察するにどうやらMaybeのインスタンス定義が渡されているようだ。 (Scalaが型クラスのインスタンスとしてimplicitパラメータで渡しているものと、ほぼ同じものだと思われる。)

Monad

最後にモナドを含むdo記法がどのようにCoreに変換されるのかを見てみる。

printArgs :: IO ()
printArgs = do
  args <- System.Environment.getArgs
  print args

-- RHS size: {terms: 7, types: 8, coercions: 0}
printArgs :: IO ()
printArgs =
  >>=
    @ IO
    $fMonadIO
    @ [String]
    @ ()
    getArgs
    (\ (args :: [String]) -> print @ [String] $dShow args)

doは糖衣構文なので脱糖後は >>= を使った式に変換されるのは予想できた。

型周りは思ったよりいろいろ混ざってきて混乱。 上から見ていく。

bind関数の定義。(型制約は除く)

>>= :: m a -> (a -> m b) -> m b

これは forall つきで表現すると

>>= :: forall m a b. m a -> (a -> m b) -> m b

となる。

よって

(@ (m :: * -> *))
(@ a)
(@ b)

が型変数として関数の引数に抽出される。 実際の対応をみてみると

-- (@ (m :: * -> *))
@ IO
-- ここはMonadのインスタンスとしてIOの定義を渡している
$fMonadIO
-- (@ a)
@ [String]
-- (@ b)
@ ()

これらを使うと >>= は下記のように具象化される。

--     getArgsより    printより
>>= :: IO [String] -> ([String] -> IO ()) -> IO ()

型変数だった部分全てに具体的な型が当てはまった。

まとめ

Haskellのプログラムはdesugar(脱糖)後にCoreという中間言語に変換される。

Coreは基本的に型付きラムダ計算(の変種)なので

  • 変数
  • 関数の定義
  • 関数の適用
  • その他 Let, Case ...

などのわずかな定義で構成される。

さらに値と型が同レベルで束縛されるラムダ抽象を用いることで

などの操作が ただの関数適用 で実現されている。

少ない規則で多彩なユースケースを実現している好例がGHCの中に潜んでいることを知ることができてよかった。

Less is more.

Yoshiko is Yohane.

Reference

下記、余談

モチベーション

Haskell Day 2016が日本で開催された時にSimon Peyton Jonesさんが"Into the Core"というタイトルでプレゼンされたらしい。 残念ながら僕は都合がつかず聞きにいけなかったけれど、同じテーマの講演が動画に収められていたのでそれをリンクしておく。

Into the Core - Squeezing Haskell into Nine Constructors by Simon Peyton Jones

早口過ぎて99%何を言っているのか僕には解らない。 けれどところどころなんとなく伝わる気がする。

プレゼンで使ったスライドは こちら

これをぼんやり聞いていて「Coreってなんだか面白いな」と思ったのがきっかけ。

これから

Coreの理論的背景になっているSystemFというラムダ計算の一種が何者なのか気になる。

GHCで用いられているSystemFCという変種については下記のリンクが参考になりそうだけど。

System F with type equality coercions

僕はそもそもラムダ計算素人なので下記の書籍を読み進める必要がありそう。

型システム入門 プログラミング言語と型の理論

最短で

  • 3章: 型無し算術式
  • 8章: 型付き算術式
  • 9章: 単純型付きラムダ計算
  • 23章: 全称型

を読めば辿り着けるように見える。

いやーほんとかなあ。。。

SMLの関数適用を構文解析する時の問題

StandardML SML Haskell compiler

まだ構文解析器で苦労している。 今回も詰まっているのは構文のconflict。

問題

これが関数適用

app : exp exp

これが二項演算子適用

infixapp : exp vid exp

この時に入力を

x y z

とすると２つの解釈ができてしまうことになる。

((x y) z)

とするネストした関数適用なのか

x y z

とする二項演算子の適用なのかParserが判断つけられない。

前者ならreduceするが後者ならshiftする。 なのでこれはshift/reduce conflictが起きていると言える。 happyはデフォルトでshiftするので二項演算子として解釈される。

これを解消したい。

解決

sml-njやmltonのgrmファイルの定義を覗いたところ

FlatAppExp : exp list

のようなデータコンストラクタを使ってとりあえずシンボルのリストとしていったん読み込んでしまうらしい。 なぜ関数適用と二項演算子適用は全然違う構造にも関わらず峻別せずに扱うのだろうと疑問に思った。

なぜだろう

SMLではfixityを自分で定義して二項演算子を作れる。

左結合か右結合かをどこかのテーブルに保存しておくことになる。(おそらくEnv的なもの？まだそのあたり解らない) こういう動的にassociativityが定義される二項演算子はパーサジェネレータでは扱えないっぽい。

なので一度解析しきってから、後でsanityチェックして弾くっぽい。

解析の途中でこのfixityのテーブルを更新しながら進めば別に解析の完了を待たなくてもいいじゃんとも思った。 けれど、それだとfixityの定義が必ず演算子の使用よりも前に定義済みである必要がある。 それは不便だろう。

ということでFlatなんたらという構造を導入してなんとか解決はできた。

追記

http://dev.stephendiehl.com/fun/008_extended_parser.html

ここを見るとinfix operatorを動的に定義していく方法が提示されているが、やはりparsecだな。ghcはどうやっているのか見てみる必要ありかな。。。

納得いってない

悪手かなと思うのは、こうした構文解析上の問題のために抽象的なデータ構造にコンストラクタを追加しなければならないという点。 せっかくきれいにsyntax objectを定義できたのにノイズが入ってしまうみたいでイマイチだなと思う。

これだと

1 + 2 + 3

みたいな入力は

[ "1", "+", "2", "+", "3" ]

のようにreduceされる。

parsecならこれをexpression builder的なAPIでうまく木構造に変換できるのだが。。。 まあ、部分的にparsec使うのはありかもしれない。

これから

あとはモジュール系の構文解析が作れればとりあえず構文解析のステージは終わりだろう。 と、言いたいところだがshift/reduceやreduce/reduceのconflictがわんさか残っている。

どうしよう。。。問題ないならこのまま進めてしまいたい。 正直conflictの解消法は未だにわかってない。

あとまだわかってないこと。

  • 構文解析終わった後のsyntax objectに位置情報を顕に保存していないけれどtype checkエラーの時に位置情報含めてレポートできるのか？
  • そもそもエラーレポートがすごくわかりにくい。後で苦労するので早めにverboseなレポート出せるようにしたい。

やりながら良かったと思うこと。

  • haskellのhappy使ってるけどmlyaccやyaccととても似ているため他のツールチェイン使った時もこのノウハウは活きるだろう
  • テストはこまめに書いているので「ここまでは動く」という証左が得られる安心感はやっぱり良い。プログラマとしてこの感覚は大事にしたい。

その他近況メモ(ぼやき)

カーネル

詳解Linuxカーネル読んでる。 メモリアドレッシングからいきなりハードル高い。

特にページングテーブルの初期化のところとか全然解らない。

Clojure

Scala勉強しなきゃ、からマッハで脱線してClojureの情報ばかり漁っている。

どっかの記事で「Clojureは大規模プロジェクトになるとメンテナンスが難しくなってきてスケールしない」みたいなこと言ってた。 そうだろうなと思う。 リファクタリングはそれほど気軽にできないだろう。

specが出てきてチェック機構は揃ってきているけれど、 それでもやはり「実行しないと結果が解らない」という制約は残る。

REPLで探索しながら直すべきところは見つけられるよ、という意見もあるかもしれないけれど リファクタリングの過程で影響のあるところ全部を検査する仕組みはやっぱり無いではなかろうか。 というかリファクタリングして壊れたところを機械的に見つける手段が無い、と言うべきか。

Clojureもそうだけど、RubyやPythonやJS使っている人たちどうしているのだろう。素朴に疑問。

とかぐだぐだ言いながらもなんかClojure好きなので勉強を続けてしまう。

好きなプログラミング言語の好きなところについて思った

Haskell Clojure Elm

改めて最近実感すること。

Haskell, Elm, Clojureほんと好き。

Scala勉強しなきゃなーと思いながらClojureを触ってしまうことが多かったのだけれど、 その理由が少しずつわかってきた。

いい言語たち

いままで少しだけ触れてきたJava, Python, Scala, Goはいずれもとても大きなユーザを抱えている。 どの言語もたくさんのユーザを得るために現場で使えるようなエコシステムをどんどん投下してあっという間に大きなユーザベースを獲得した。

プログラミングのしやすさを大事にして、誰でもすんなり入門できるように設計されている。 僕が入門できるくらいだから本当に敷居が低くて、けれどどんなやりたいことも実現させてくれるいい言語ばかりだ。 押し付けがましい思想も少ない。

たのしい言語たち

一方でHaskell, Elm, Clojureはちょっと独特だ。

HaskellではMonadicなプログラミングやSTM, デフォルト遅延評価など今まで触れたこともないようなパラダイムで溢れていた。

ElmではElm Architectureという一見してみると強い制約のもとでWeb UIを構築しなければいけなかった。

ClojureではREPL駆動開発やtransducer, 状態のオペレーション(STM, Atom, Agentなど)という独特なキーワードが骨子になっている。

(あ、全部関数型プログラミングだ。。。)

いずれも今までの自分には聞いたこともないような概念ばかりで、きっと解らなくてすぐに挫折してしまうだろうと思った。 だけど全然そんなことはなかった。むしろ楽しかった。

やりたいことが手元にあって、それを実現するためにどうしようかと考える時、Haskell, Elm, Clojureではまず素直に落とし込めない。 どんなやり方があるのか調べて、どれがその言語らしい XXX way なのかを知っていかなければいけない。 本当に手間がかかることが多い。

なのになんでこんな楽しいのだろう。進まない。進まないのに。

簡単≠たのしい

その制約のせいか、「できた！」と思った時の瞬間が本当に嬉しい。やっていることは全然大したことない。 SpringBootとかDjangoとか使えば瞬殺なのだろう。

でも、なんというか、その言語の思想に沿うように実装できた時の嬉しさは要求を鮮やかに実現できた時の歓喜とは別の何かだ。 3Dプリンターで模型を切り出すのではなくて、彫刻刀で大仏を彫り出すような変なドグマの混じったカタルシスを感じる。

何ができるかではなくて、どうやるかが楽しい。 ほんと、仕事としてプログラマやっている人間としては全然駄目だと思う。 実際問題、顧客の要求を低コストで十分に実装する能力や判断力の方が絶対にお金は入るはずなんだ。 成果物や収益から逸脱して、作法や流儀や過程に楽しみを見出してコストを支払うなんて多分駄目なはずなんだ。

でも何故だろうか、遠回りなのに美しい道が用意されているように見えるプログラミング言語ばかり好きになってしまう。 マーケットとか人材の需要とかじゃなくて、思想や信念や流儀に見え隠れする怪しさ(妖しさ？)に惹かれてしまう。

本当はScalaやPythonやGoに触れて経験を積んだ方がきっとすぐに応用に入れる場面も多いはずなのに。 どうもそういう打算が働かず、ただただ楽しいと思うプログラミング言語に傾倒していくのを自ら止められずうろうろしている。

幸い、Haskell, Elm, Clojureはプロダクションでの採用事例も増えてきている。いずれ自分が書いたHaskell, Elm, Clojureのコードがプロダクション環境で動く日が来たらいいなあ、と思う。

Erlangとかもなんだか光背が見える言語だ。。。気になる。

ネットワーク機器の制御とかでHaskell, Elm, Clojureあたり使っている会社の仕事とかあったらいいなー。 ネットワーク(特にバックボーン)業界はだいたいPythonかJava, Goなのでもう少し僕が好きなプログラミング言語の実装増えてこないかなあ。

(自分で書いていけってことか。。。)